Quin és el numero més gran que se t’acut al pensar en números algebraics (és a dir en números els quals sòn solucions d’un polinomi no nul de coeficients racionals)? El googol (10^100), el googlolplex (10^10^100), el número de Skewes, el número de Monses o el de Shannon? Que tal si et dic que hi ha un número molt més gran del que podries respondre? Aquest es el numero de graham, tant gran que ni tant sols el podem visualitzar.
 |
| Imatge extreta de: https://www.labrujulaverde.com/wp-content/uploads/2019/01/shutterstock_268623200.jpg |
El número de Graham va ser teoritzat per Ronald Graham l’any 1977 intentant trobar la solució al “problema de Ramsey”. Graham i Rothschild, 1971 van demostrar que aquesta qüestió té una solució N*, amb l’acotació 6 ≤ N* ≤ N, sent N un número determinat molt gran, Graham va seguir l’estudi i va acabar determinant que aquest número N corresponia a G, el número de Graham. Si no el podem visualitzar com sabem que existeix? Ens permet representar altres dimensions? O és l’expressió de múltiples dimensions? Qui millor per respondre aquestes preguntes que el mateix Ronald Graham, en aquest vídeo ens explica com sorgeix aquest número.
 |
| Imatge extreta de: https://w7.pngwing.com/pngs/560/596/png-transparent-graham-s-number-large-numbers-googolplex-mathematics-too-far-and-book-angle-rectangle-triangle.png |
I com l’anotem? Com qualsevol número gran per anotar-lo i que no ens ocupi mitja plana, fem ús d’exponencials, així doncs s’usa una notació especial per aquest número, usant la notació de fletxes de Knuth. Aquesta expressa les potencies amb fletxes, d’aquesta manera, com podem observar:
3↑3 = 3*3*3 = 27
3↑↑3 = 3↑(3↑3)=3(e 27) = 7.625.597.484.987
3↑↑↑3= 3↑↑3↑↑3 = 3(e 7.625.597.484.987) = major que un googloplex
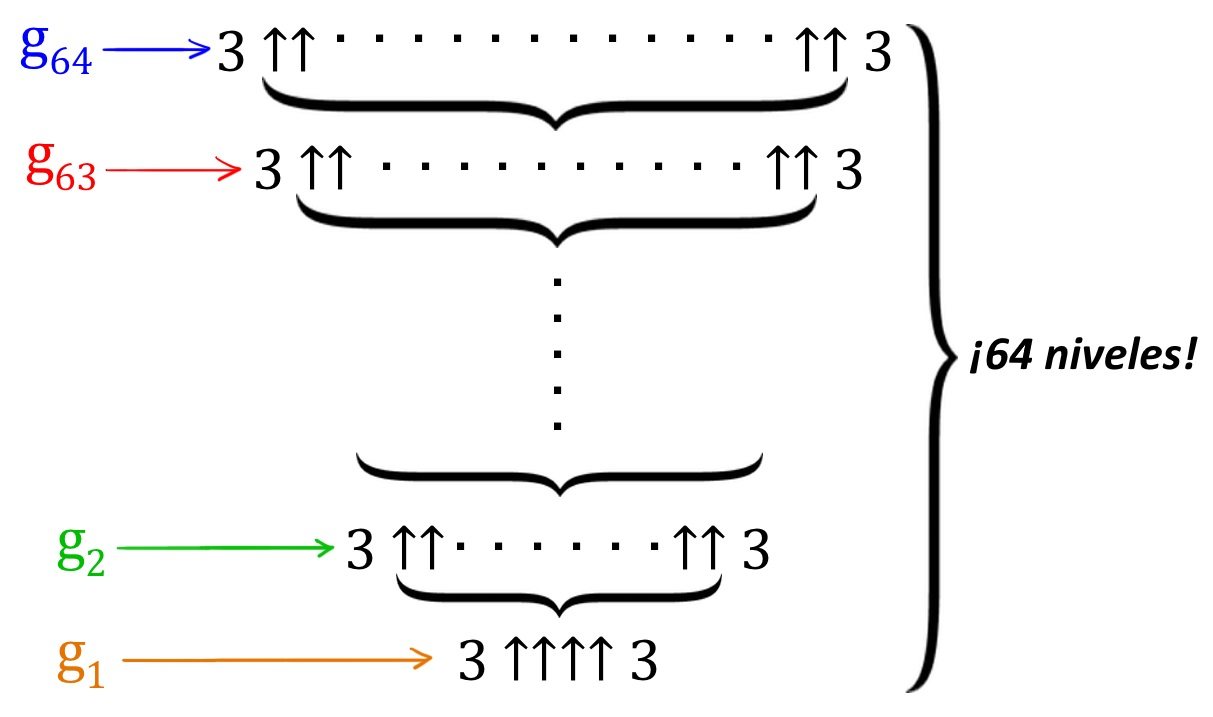
Aquest número G equival a g64, és a dir 64 passos, on g1 correspon a: g1= 3↑↑↑↑3 =3 elevat a un nombre que és igual a elevar 7,6 trilions de vegades 3.
 |
| Imatge extreta de: https://www.neoteo.com/wp-content/uploads/2019/06/03-10.jpg |
Amb la qual cosa aquest número es extremadament llarg, aquí deixo unes quantes xifres (500 últims) números:
02425950695064738395657479136519351798334535362521430035401260267716226721604198106522631693551887803881448314065252616878509555264605107117200099709291249544378887496062882911725063001303622934916080254594614945788714278323508292421020918258967535604308699380168924988926809951016905591995119502788717830837018340236474548882222161573228010132974509273445945043433009010969280253527518332898844615089404248265018193851562535796399618993967905496638003222348723967018485186439059104575627262464195387
I perquè és voldria usar tal número? Com hem dit és la solució a un problema matemàtic que estaven treballant, concretament aquest número és el límit superior de la solució de n-dimensions.
Comparat amb el número d’àtoms existents en l’univers observable 10^82àatoms, aquest número es veu ridículament petit al comparar-lo amb el número de Graham.
"El Número de Graham realment no està més a prop de l'infinit que el número u. Simplement no has començat encara. Fins i tot encara que et prengués molts passos per arribar al Número de Graham, es porta moltíssim més, infinitament més, arribar a l'infinit"
- Roland L. Graham
Bibliogrfía: